位置ベース流体(Position Based Fluids)†
粒子法を用いた流体シミュレーションにおいて重要な要素となるのが
非圧縮性の強制である.
非圧縮性とは流体の密度が流れによって空間的にも時間的にも変化しないことを表し,
水のような液体はもちろん,
流速が音速より十分小さいならば空気も非圧縮性流体と考えることができる
(ちなみに音速に近くなると空気は圧縮する,
音速に達した飛行機が発する衝撃波いわゆるソニックブームは空気が圧縮することで引き起こされる).
非圧縮性のための様々な方法(MPS,WCSPH,PCISPH,IISPHなど)が提案されているが,
それらに比べて非常に高速かつ安定した計算が可能なのが位置ベース流体法(Position Based Fluids, 以下PBF)¬e{Macklin2013:M. Macklin and M. Muller, "Position based fluids" ACM Trans. Graph., 32, pp.104:1-104:12, 2013.};
である.
PBFは位置ベース法(Position-based method)¬e{Muller2007:M. Muller, B. Heidelberger, M. Hennix and J. Ratcliff, "Position based dynamics", J. Vis. Comun. Image Represent., 18, pp.109-118, 2007.};
の一種である.
位置ベース法では従来の力学ベースの方法と異なり,位置(物体の空間座標値)を満たすべき制約に従って直接変更する方法である
力学ベースでは支配方程式に従い加速度->速度->位置と変更していくため,
それぞれで積分に伴う誤差の蓄積が発生するが位置に直接制約をかける位置ベース法はそれがない.
ただし,頂点や粒子の位置関係に基づく制約をかけるためどちらかというと幾何学的な方法で,
あまり物理的ではないのではないかという議論もある.
位置ベース法の基本†
PBFの前に基本となる位置ベース法の考え方を説明する.
まず,移動する計算点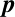 に対して,その座標値そのものに制約条件
に対して,その座標値そのものに制約条件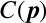 を掛けることを考える.
を掛けることを考える.
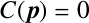 の条件が常に満たされているとすると,
粒子が微少量
の条件が常に満たされているとすると,
粒子が微少量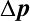 移動した後もこの条件は満たされているということになるので,
移動した後もこの条件は満たされているということになるので,
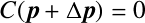 となる.
これをテイラー展開してやれば,
となる.
これをテイラー展開してやれば,
となる.2次以降の項を無視すれば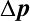 に関する方程式が得られる.
に関する方程式が得られる.
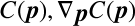 は制約として定義しているのでそこから計算できる.
いま,
は制約として定義しているのでそこから計算できる.
いま,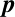 を粒子の中心座標とすると求めるべき未知数の数は
粒子数を
を粒子の中心座標とすると求めるべき未知数の数は
粒子数を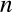 としたら3次元空間の場合
としたら3次元空間の場合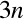 となる.
一方で
となる.
一方で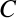 が各粒子ごとに計算される(つまり
が各粒子ごとに計算される(つまり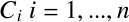 )ならば,
上記の方程式の数は
)ならば,
上記の方程式の数は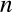 なので未知数
なので未知数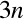 に対して少なすぎて解が定まらない
(疑似逆行列などを使ってできないことはない).
そこで
に対して少なすぎて解が定まらない
(疑似逆行列などを使ってできないことはない).
そこで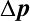 に対して別の制約をかける.
に対して別の制約をかける.
計算点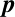 が運動方程式に従って移動していると考えると,
ここでの
が運動方程式に従って移動していると考えると,
ここでの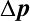 はその運動とは別の制約
はその運動とは別の制約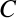 を満たすための移動となる.
そうすると元の運動(平行移動と回転)を阻害しないような移動方向,
言い換えると平行移動と回転運動量を保存するような移動方向を定める必要がある.
制約
を満たすための移動となる.
そうすると元の運動(平行移動と回転)を阻害しないような移動方向,
言い換えると平行移動と回転運動量を保存するような移動方向を定める必要がある.
制約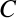 がこれらの運動の状態に全く作用されない(依存しない)と考えるならば,
その傾き
がこれらの運動の状態に全く作用されない(依存しない)と考えるならば,
その傾き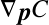 はこれらの運動方向に対して垂直な方向となる.
つまり,
はこれらの運動方向に対して垂直な方向となる.
つまり,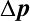 の方向を
の方向を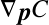 となるような制約を掛けてやればよいことになる.
これはちょうど制約付きの最適化問題になるのでラグランジュ乗数
となるような制約を掛けてやればよいことになる.
これはちょうど制約付きの最適化問題になるのでラグランジュ乗数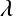 を導入して,
を導入して,
とする.
これを上の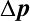 に関する方程式に代入して整理すると,
に関する方程式に代入して整理すると,
となる.求めた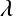 を
を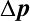 の式に代入すれば制約を満たすための移動ベクトルが分かるので,
それで計算点位置を修正してやればよい.
複数の計算点が絡む場合は1回の修正では制約を満たすことは難しいので,
上記の式による制約を条件を満たすまで反復処理する.
の式に代入すれば制約を満たすための移動ベクトルが分かるので,
それで計算点位置を修正してやればよい.
複数の計算点が絡む場合は1回の修正では制約を満たすことは難しいので,
上記の式による制約を条件を満たすまで反復処理する.
位置ベース法の粒子法への適用†
さて,話を粒子法の場合に戻そう.
まず,非圧縮性条件が満たすべき制約(Constraint)を考える.
流体が圧縮しないということはその密度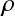 が初期密度
が初期密度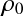 から変化しないということであり,
つまり,条件としては
から変化しないということであり,
つまり,条件としては である.これを変形して位置
である.これを変形して位置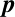 に関する制約
に関する制約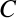 として定式化すると,
として定式化すると,
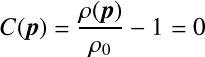 ・・・(1)
・・・(1)
となる.
ここでは粒子法の一種であるSPH法を使ってある粒子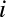 の密度
の密度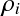 を求める.
を求める.
ここで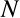 は粒子
は粒子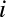 の近傍粒子の集合,
の近傍粒子の集合,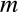 は粒子質量,
は粒子質量,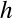 は有効半径である.
近傍粒子数を
は有効半径である.
近傍粒子数を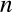 とすると粒子
とすると粒子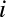 の密度に関する制約は近傍粒子座標
の密度に関する制約は近傍粒子座標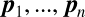 の
関数となるので,
の
関数となるので,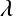 の計算式は以下のようになる.
の計算式は以下のようになる.
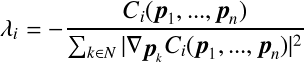 ・・・(2)
・・・(2)
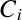 は密度
は密度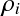 の式を式(1)に代入すれば計算できる.
の式を式(1)に代入すれば計算できる.
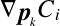 も同様で,SPH法における勾配値は単に重み関数
も同様で,SPH法における勾配値は単に重み関数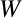 の勾配をとればよいので,
の勾配をとればよいので,
となる.
この式で注意しないといけないのは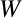 は
は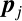 と
と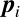 (と
(と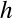 )に関する関数なので,
)に関する関数なので,
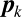 で微分したときに0にならないのは
で微分したときに0にならないのは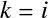 と
と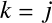 の場合だけである.
そうすると上記の式はさらに書き下すことができて,
の場合だけである.
そうすると上記の式はさらに書き下すことができて,
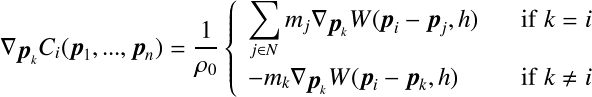 ・・・(3)
・・・(3)
となる.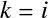 の時は
の時は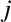 に関わらず
に関わらず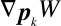 は
は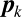 を含むのでそのまま計算すればよい.
を含むのでそのまま計算すればよい.
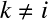 の場合は
の場合は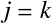 となったときだけ
となったときだけ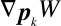 を含むのでそれだけ計算する
(マイナスの符号がついているのは
を含むのでそれだけ計算する
(マイナスの符号がついているのは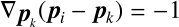 なので).
また,粒子質量
なので).
また,粒子質量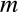 がすべての粒子で一定ならば
がすべての粒子で一定ならば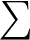 の外に出せて,
最終的に
の外に出せて,
最終的に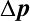 の計算ではすべて打ち消されるので計算上は省略してもよい.
の計算ではすべて打ち消されるので計算上は省略してもよい.
式(2)と式(3)により各粒子のラグランジュ乗数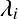 が計算されるので,
これらから各粒子の位置修正量
が計算されるので,
これらから各粒子の位置修正量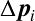 を求める.
このとき近傍粒子への影響と近傍粒子からの影響が非対称にならないようする(SPH法の圧力項等と同じ).
を求める.
このとき近傍粒子への影響と近傍粒子からの影響が非対称にならないようする(SPH法の圧力項等と同じ).
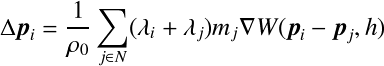 ・・・(4)
・・・(4)
先ほども説明したように質量一定ならばこちらの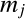 も省略できる.
も省略できる.
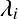 と
と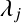 の平均をとるならば
の平均をとるならば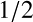 をつけるところだが,
SOR法の加速緩和係数と同じ役割を果たすようで,ない方が収束は速くなる.
をつけるところだが,
SOR法の加速緩和係数と同じ役割を果たすようで,ない方が収束は速くなる.
張力の安定化†
SPH法では近傍粒子数が少ない場合に負の圧力が発生して粒子同士が過度に集まってしまう
(particle clusteringやparticle stackingと呼ばれている)現象が発生する.
PBFではこれを解決するためにMonaghan
¬e{Monaghan2000:J. Monaghan, "SPH without a Tensile Instability", Journal of Computational Physics, 159, pp.290-311, 2000.};
が提案した以下のような項を式(4)に追加している.
式中のパラメータの値としては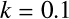 ,
,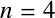 ,
,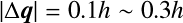 あたりがよいようである.
式(4)の
あたりがよいようである.
式(4)の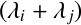 の部分を
の部分を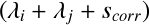 とするのだが,
Monaghanの元の論文では
とするのだが,
Monaghanの元の論文では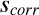 は加速度なので位置修正に直接使うのはおかしくなるので,
下記の私の実装では
は加速度なので位置修正に直接使うのはおかしくなるので,
下記の私の実装では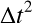 を掛けてある.
を掛けてある.
境界粒子†
前述のparticle stackingの問題は固体境界付近でも発生する.
粒子と固体境界の単純な衝突処理だけだと固体内に粒子が存在しないため,
境界付近に粒子が集まってしまう.
それを解決する一つの方法が固体境界内に位置固定の粒子(境界粒子)を散布することである.
通常,境界粒子は有効半径に合わせて複数層配置するが,
Akinciらの方法¬e{Akinci2012:N. Akinci, M. Ihmsen, G. Akinci, B. Solenthaler and M. Teschner, "Versatile rigid-fluid coupling for incompressible SPH", ACM Trans. Graph., ACM, 31, pp.62:1-62:8, 2012.};
を使えば,仮想的な体積を事前に計算しておくことで1層だけで済ますことができる.
境界に沿って粒子を配置した後,境界粒子だけを使って以下の仮想体積を計算して格納しておく.
そして,PBFでも計算時に境界粒子の質量を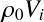 としてやればよい
(詳しい式などはこちらの論文を参照).
としてやればよい
(詳しい式などはこちらの論文を参照).
実装例†
Visual Studio 2012 + CUDA7.5の環境で作成したコードは以下.
- ビルドするのに必要なライブラリ
freeglut, GLEW, CUDA, (OpenVDB)
各ライブラリについてはライブラリのインストールを参照.
- 簡単な説明&注意事項
- GUIツールキットとしてFLTKを用いている.
- rx_fltk_glcanvas.hの55行目
#define RX_USE_GPU
をコメントアウトするとCPUで計算する.
- OpenVDBはポリゴンモデルを読み込んでその内部に境界粒子を配置する場合に必要.使用する場合はプロプロセッサ定義にRX_USE_OPENVDBを追加する.
- モデルの読み込み自体は3Dモデルファイルの入出力のrx_model.libを使っている.
- Visual Studioから実行する場合は,作業ディレクトリを"../../bin"にしておく.
- "s"キー or Start/Stopボタンでシミュレーションスタート/ストップ.
- F1〜F9キー or Sceneメニューからシーン切替可能.binフォルダに"sph_scene_*.cfg"という名前のファイルがあり,
これがシーンを記述するファイル.デフォルトでは4つのシーンが入っている.
- CUDAはv7.5で動作を確認している.
- ポリゴンモデルを固体境界とした場合に境界粒子配置のためにOpenVDBを用いている(正確には境界粒子を配置するための陰関数場生成のため).デフォルトではOpenVDB使用をOFFにしているので,ポリゴン境界に粒子を配置したい場合はプリプロセッサでRX_USE_OPENVDBを定義するか,rx_sph_solid_poly.cppの先頭でdefineすること.
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)