ホーナー法

2分法やニュートン法を使って以下の次の代数方程式を解くときの演算回数を考える．

の値を計算する際の乗算回数は回で 加算が回である． 乗算回数がの2乗で増えるため，たとえば，では55回だが，だと5050回にもなる．

乗算回数を少なくするために代数方程式を以下のように変形する．

この場合，一番内側の括弧内から計算していくと，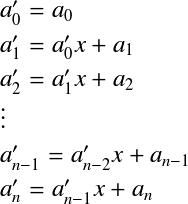

となり，最終的にとなる． このときの乗算回数は回，加算も回である． 特にが大きな時に計算回数を大幅に減らすことができる． たとえば，乗算回数はで10回，でも100回で済む． この計算方法はホーナー(Horner)法と呼ばれる．

ホーナー法で代数方程式の値とその導関数を求めるコード例を以下に示す．

/*!
 * ホーナー法で代数方程式の値を計算
 * @param[in] x 変数
 * @param[in] b 係数
 * @param[in] n 方程式の次数
 * @return 代数方程式の値
 */
template<class T>
inline T func_h(double x, const vector<T> &b, int n)
{
    T f = b[0];
    for(int i = 1; i <= n; ++i){
        f = b[i]+f*x;
    }
    return f;
}
/*!
 * ホーナー法で代数方程式の導関数値を計算
 * @param[in] x 変数
 * @param[in] b 係数
 * @param[in] n 方程式の次数
 * @return 代数方程式の導関数値
 */
template<class T>
inline T dfunc_h(double x, const vector<T> &b, int n)
{
    T df = n*b[0];
    for(int i = 1; i <= n-1; ++i){
        df = (n-i)*b[i]+df*x;
    }
    return df;
}

テンプレート関数にしているのはDKA法で複素数を扱う関係上，様々な型に対応できるようにしたいためである．