![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
LU分解†これまでn元連立1次方程式 を直接法,反復法などで解くことだけを考えてきた. それでは実際の問題ではこのような線形システムはどのように扱われるだろうか. たとえば,制御の分野ではシステムの状態変化を捉えるために用いている. 係数行列Aがシステム内部を表し,右辺の定数ベクトルbで外乱などの状態を表す. システム内部が変わらず,外の状態が様々に変化したときの状態を知りたいとき, 係数行列Aは変化せず,bのみが変わるだけである. このように係数行列が固定で右辺の定数ベクトルだけが変化するということは, 物理学などの他の分野でも多くある. このとき,係数行列Aを解きやすい形に分解しておけば,計算量を大幅に減らすことができる. ここではそのような分解の一つであるLU分解について述べる. n元連立1次方程式の係数行列を考える.  これを以下の下三角行列(lower triangular matrix) L と 上三角行列 (upper triangular matrix) U に分解する. 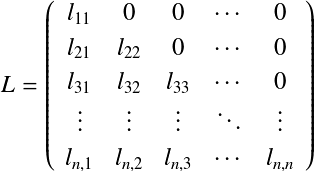  ここで, LU分解した行列で連立1次方程式を解くことを考える.
まず,
となる.Lは下三角行列であるので,1行目から順番に代入していくことで,
容易に LU分解の手順†係数行列AをLU分解するためには,以下の式を1行目から順番に適用していく. 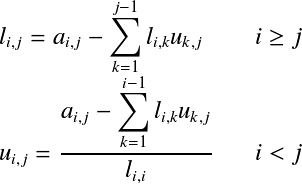 メモリを節約するために,LU分解した結果を以下のように1つの行列に格納する. 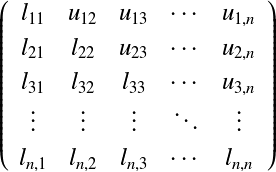 LU分解の実装†LU分解をC++で実装した例を以下に示す. /*!
* LU分解(ピボット交換なし)
* - 行列A(n×n)を下三角行列(L:Lower triangular matrix)と上三角行列(U:Upper triangular matrix)に分解する
* - L: i >= j, U: i < j の要素が非ゼロでUの対角成分は1
* - LとUを一つの行列にまとめた形で結果を返す
* @param[inout] A n×nの係数行列.LU分解した結果を格納する.
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int LUDecomp(vector< vector<double> > &A, int n)
{
if(n <= 0) return 0;
for(int i = 0; i < n; ++i){
// l_ijの計算(i >= j)
for(int j = 0; j <= i; ++j){
double lu = A[i][j];
for(int k = 0; k < j; ++k){
lu -= A[i][k]*A[k][j]; // l_ik * u_kj
}
A[i][j] = lu;
}
// u_ijの計算(i < j)
for(int j = i+1; j < n; ++j){
double lu = A[i][j];
for(int k = 0; k < i; ++k){
lu -= A[i][k]*A[k][j]; // l_ik * u_kj
}
A[i][j] = lu/A[i][i];
}
}
return 1;
}
LU分解で連立1次方程式を解く手順†LU分解で連立1次方程式を解く方法は上でも述べたがここではより具体的な手順について説明する. LU分解で連立1次方程式を解く手順は以下である.
LU分解を用いた連立1次方程式の解法の実装†LU分解で連立1次方程式を解くコードをC++で実装した例を以下に示す. /*!
* LU分解した行列a(n×n)から前進代入・後退代入によりA・x=bを解く
* @param[in] A LU分解された行列
* @param[in] b 右辺ベクトル
* @param[out] x 結果ベクトル
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int LUSolver(const vector< vector<double> > &A, const vector<double> &b, vector<double> &x, int n)
{
if(n <= 0) return 0;
// 前進代入(forward substitution)
// LY=bからYを計算
for(int i = 0; i < n; ++i){
double bly = b[i];
for(int j = 0; j < i; ++j){
bly -= A[i][j]*x[j];
}
x[i] = bly/A[i][i];
}
// 後退代入(back substitution)
// UX=YからXを計算
for(int i = n-1; i >= 0; --i){
double yux = x[i];
for(int j = i+1; j < n; ++j){
yux -= A[i][j]*x[j];
}
x[i] = yux;
}
return 1;
}
コレスキー分解†LU分解では係数行列を と分解できる下三角行列Lが存在する.この式はLU分解で 上式を成分で表す.
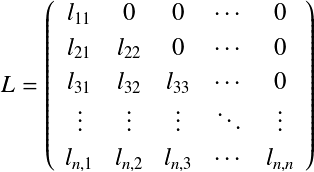 とすると, となる. 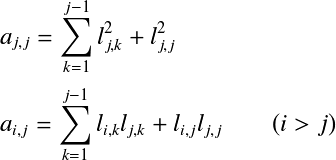 よって,以下の式を 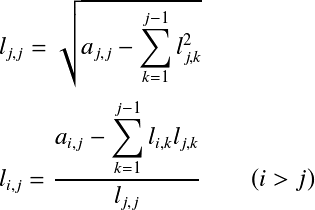 たとえば, 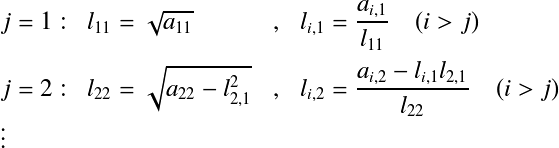 という手順で計算していく. 対称行列に限定されるものの,LU分解と異なり,Lだけを求めればよいので計算手順は半分で済む. 下三角行列Lが求まったら,LU分解のときと同様に前進代入,後退代入の手順で連立1次方程式 コレスキー分解では計算に平方根が含まれており,平方根の中が正でなければならない.
また,0でも 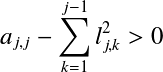 でなければならない. この条件は対称正定値行列のときには満たされることが証明されているが, 正定値でない対称行列では問題がある. また,計算コストがかかる平方根の計算もできれば避けたい. そのため,コレスキー分解はあまり使われず, 以下で述べる修正コレスキー分解や不完全コレスキー分解がよく用いられる. 修正コレスキー分解†コレスキー分解の平方根の問題を解決するために改良を加えられたのが 修正コレスキー分解(Modified Cholosky decomposition)である. まず,コレスキー分解の下三角行列  この式をコレスキー分解に当てはめると, ここで, と分解できる.これが修正コレスキー分解である. この式を成分で表すと以下となる. コレスキー分解の時と同様に 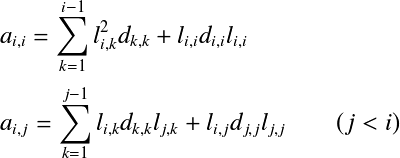 ここで, 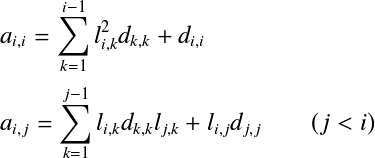 よって,以下の式を 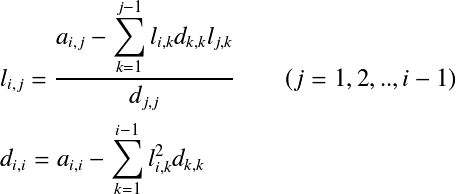 ただし, L,Dが求まったら,LU分解のときと同様に前進代入,後退代入の手順で連立1次方程式 計算式をみてもわかるように,L,Dに分解することで対角成分の2乗項 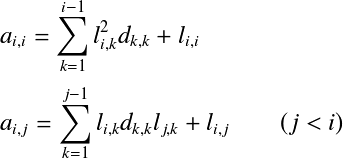 よって,以下の式を 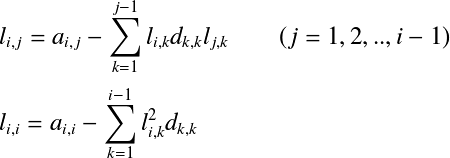 ここで, 修正コレスキー分解の実装†修正コレスキー分解をC++で実装した例を以下に示す.
それぞれ, /*!
* 修正コレスキー分解(modified Cholesky decomposition)
* - 対称行列A(n×n)を下三角行列(L:Lower triangular matrix)と対角行列の積(LDL^T)に分解する
* - l_ii = 1とした場合
* - L: i > jの要素が非ゼロで対角成分は1
* @param[in] A n×nの対称行列
* @param[out] L 対角成分が1の下三角行列
* @param[out] d 対角行列(対角成分のみ)
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int ModifiedCholeskyDecomp(const vector< vector<double> > &A, vector< vector<double> > &L, vector<double> &d, int n)
{
if(n <= 0) return 0;
d[0] = A[0][0];
L[0][0] = 1.0;
for(int i = 1; i < n; ++i){
// i < k の場合
for(int j = 0; j < i; ++j){
double lld = A[i][j];
for(int k = 0; k < j; ++k){
lld -= L[i][k]*L[j][k]*d[k];
}
L[i][j] = (1.0/d[j])*lld;
}
// i == k の場合
double ld = A[i][i];
for(int k = 0; k < i; ++k){
ld -= L[i][k]*L[i][k]*d[k];
}
d[i] = ld;
L[i][i] = 1.0;
}
return 1;
}
/*!
* 修正コレスキー分解(modified Cholesky decomposition)
* - 対称行列A(n×n)を下三角行列(L:Lower triangular matrix)と対角行列の積(LDL^T)に分解する
* - l_ii * d_i = 1とした場合
* - L: i > jの要素が非ゼロで対角成分は1
* @param[in] A n×nの対称行列
* @param[out] L 対角成分が1の下三角行列
* @param[out] d 対角行列(対角成分のみ)
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int ModifiedCholeskyDecomp2(const vector< vector<double> > &A, vector< vector<double> > &L, vector<double> &d, int n)
{
if(n <= 0) return 0;
L[0][0] = A[0][0];
d[0] = 1.0/L[0][0];
for(int i = 1; i < n; ++i){
for(int j = 0; j <= i; ++j){
double lld = A[i][j];
for(int k = 0; k < j; ++k){
lld -= L[i][k]*L[j][k]*d[k];
}
L[i][j] = lld;
}
d[i] = 1.0/L[i][i];
}
return 1;
}
不完全コレスキー分解†実際の問題を線形システムでモデル化した場合,nが非常に大きい場合が多い.
たとえば,数値流体力学において有限差分法を用い,
計算空間を 一方,こういった問題にみられる行列の性質として,疎行列というものがある. 疎行列は対角成分付近にのみ値が有り,非対角成分のほとんどが0の行列である. 例としてあげた圧力のポアソン方程式の行列も対称な疎行列となる. このような疎行列に対し,その要素が0ならば,その位置のLの要素を0にするといった近似を置くことで, 高速に,かつ,疎行列の性質を保ったまま変換するのが, 不完全コレスキー分解(Incomplete Cholosky decomposition : IC法)である. たとえば,係数行列Aの0要素の位置のLの要素を0とする不完全コレスキー分解の場合,
修正コレスキー分解の計算式( 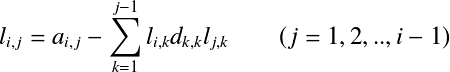 に対して,以下の条件付で計算を行う.
なお,この方法はあくまで近似値を求めているので,正確な分解ではないことに注意. 不完全コレスキー分解の実装†以下は不完全コレスキー分解のコード例である. /*!
* 不完全コレスキー分解(incomplete Cholesky decomposition)
* - 対称行列A(n×n)を下三角行列(L:Lower triangular matrix)と対角行列の積(LDL^T)に分解する
* - l_ii = 1とした場合
* - L: i > jの要素が非ゼロで対角成分は1
* - 行列Aの値が0である要素に対応する部分を飛ばす
* @param[in] A n×nの対称行列
* @param[out] L 対角成分が1の下三角行列
* @param[out] d 対角行列(対角成分のみ)
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int IncompleteCholeskyDecomp(const vector< vector<double> > &A, vector< vector<double> > &L, vector<double> &d, int n)
{
if(n <= 0) return 0;
d[0] = A[0][0];
L[0][0] = 1.0;
for(int i = 1; i < n; ++i){
// i < k の場合
for(int j = 0; j < i; ++j){
if(fabs(A[i][j]) < 1.0e-10) continue;
double lld = A[i][j];
for(int k = 0; k < j; ++k){
lld -= L[i][k]*L[j][k]*d[k];
}
L[i][j] = (1.0/d[j])*lld;
}
// i == k の場合
double ld = A[i][i];
for(int k = 0; k < i; ++k){
ld -= L[i][k]*L[i][k]*d[k];
}
d[i] = ld;
L[i][i] = 1.0;
}
return 1;
}
以下は /*!
* 不完全コレスキー分解(incomplete Cholesky decomposition)
* - 対称行列A(n×n)を下三角行列(L:Lower triangular matrix)と対角行列の積(LDL^T)に分解する
* - l_ii * d_i = 1とした場合
* - L: i > jの要素が非ゼロで対角成分は1
* - 行列Aの値が0である要素に対応する部分を飛ばす
* @param[in] A n×nの対称行列
* @param[out] L 対角成分が1の下三角行列
* @param[out] d 対角行列(対角成分のみ)
* @param[in] n 行列の大きさ
* @return 1:成功,0:失敗
*/
int IncompleteCholeskyDecomp2(const vector< vector<double> > &A, vector< vector<double> > &L, vector<double> &d, int n)
{
if(n <= 0) return 0;
L[0][0] = A[0][0];
d[0] = 1.0/L[0][0];
for(int i = 1; i < n; ++i){
for(int j = 0; j <= i; ++j){
if(fabs(A[i][j]) < 1.0e-10) continue;
double lld = A[i][j];
for(int k = 0; k < j; ++k){
lld -= L[i][k]*L[j][k]*d[k];
}
L[i][j] = lld;
}
d[i] = 1.0/L[i][i];
}
return 1;
}
参考文献†
|