![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
ガウスの消去法†ガウスの消去法(Gaussian elimination)と呼ばれる方法では, 前進消去と後退代入という2段階の計算により解を求める. 一般的な(中学校で習う)解き方の一つに加減法というものがある. たとえば,以下のような連立方程式で考える.  加減法では片方の式の両辺に実数をかけて,係数を合わせて,加減算する. ここでは下の式の両辺を2倍して,上の式から引くことにする. 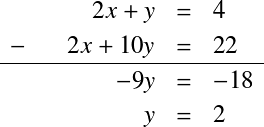 あとは, これを行列で表すと, に対して,2行目に という形にする.そして,一番下の行から未知数を解いて代入していく. 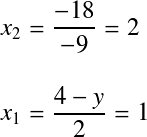 前半の処理では係数行列 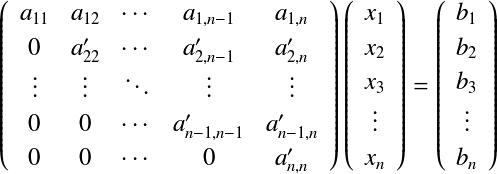 この処理のことを前進消去(forward elimination)と呼ぶ.
前進消去により,未知数 ガウスの消去法の実装†ガウスの消去法を  この行列は拡大行列と呼ばれる. 拡大行列の要素を とする.ここで,C,C++で実装することを考えて要素番号を0始まりにしている. 今後,実装の説明では0で始まるインデックスを用いるので注意. 前進消去は次の式で表される. ここで, 上式により // 前進消去(forward elimination)
// - 対角要素をのぞいた左下要素をすべて0にする(上三角行列にする)
for(int k = 0; k < n-1; ++k){
double akk = A[k][k];
for(int i = k+1; i < n; ++i){
double aik = A[i][k];
for(int j = k; j < n+1; ++j){ // 確認のため左下要素が0になるようにj=kとしたが,実際にはj=k+1でよい
A[i][j] = A[i][j]-aik*(A[k][j]/akk);
}
}
}
2次元配列A[n][n+1]には係数行列と定数ベクトルが格納されている. 次に後退代入の式を以下に示す. 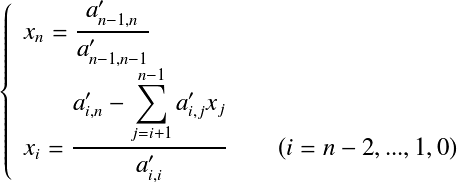 後退代入のC++のコード例を以下に示す. // 後退代入(back substitution)
// - x_nの解はb_n/a_nn,x_nをさらにn-1行の式に代入することでx_(n-1)を求める.
// - この作業を1行目まで続けることですべての解を得る.
A[n-1][n] = A[n-1][n]/A[n-1][n-1];
for(int i = n-2; i >= 0; --i){
double ax = 0.0;
for(int j = i+1; j < n; ++j){
ax += A[i][j]*A[j][n];
}
A[i][n] = (A[i][n]-ax)/A[i][i];
}
計算された結果は別の配列でなくA[i][n]に格納しているので注意. ガウスの消去法の全体のコードは以下. /*!
* ガウスの消去法(ピボット交換なし)
* @param[inout] A n×nの係数項とn×1の定数項(b)を併せたn×(n+1)の行列.n+1列目に解が入る.
* @param[in] n n元連立一次方程式
* @return 1:成功
*/
int GaussElimination(vector< vector<double> > &A, int n)
{
// 前進消去(forward elimination)
// - 対角要素をのぞいた左下要素をすべて0にする(上三角行列にする)
for(int k = 0; k < n-1; ++k){
double akk = A[k][k];
for(int i = k+1; i < n; ++i){
double aik = A[i][k];
for(int j = k; j < n+1; ++j){ // 確認のため左下要素が0になるようにj=kとしたが,実際にはj=k+1でよい
A[i][j] = A[i][j]-aik*(A[k][j]/akk);
}
}
}
// 後退代入(back substitution)
// - x_nの解はb_n/a_nn,x_nをさらにn-1行の式に代入することでx_(n-1)を求める.
// - この作業を1行目まで続けることですべての解を得る.
A[n-1][n] = A[n-1][n]/A[n-1][n-1];
for(int i = n-2; i >= 0; --i){
double ax = 0.0;
for(int j = i+1; j < n; ++j){
ax += A[i][j]*A[j][n];
}
A[i][n] = (A[i][n]-ax)/A[i][i];
}
return 1;
}
標準の2次元配列の代わりにSTLのvectorを使っている. ピボット選択†ガウスの消去法における前進消去の式をもう一度みてみる. 右辺の第2項に この問題に対処するために,ピボット(pivot:枢軸)選択(pivotal elimination method),もしくは,ピボッティング(pivoting)
と呼ばれる方法を説明する.
まず,連立方程式において式の順番は交換可能であることに注目する.
つまり, 以下にピボット選択を含めたガウス消去法のコード例を示す. /*!
* ピボット選択(Pivoting)
* - 行入れ替えだけの部分的ピボッティング
* @param[inout] A n×nの係数項とn×1の定数項(b)を併せたn×(n+1)の行列
* @param[in] n n元連立一次方程式
* @param[in] k 対象行
* @return 1:成功
*/
inline void Pivoting(vector< vector<double> > &A, int n, int k)
{
// k行目以降でk列目の絶対値が最も大きい要素を持つ行を検索
int p = k; // 絶対値が最大の行
double am = fabs(A[k][k]);// 最大値
for(int i = k+1; i < n; ++i){
if(fabs(A[i][k]) > am){
p = i;
am = fabs(A[i][k]);
}
}
// k != pならば行を交換(ピボット選択)
if(k != p) swap(A[k], A[p]);
}
/*!
* ガウスの消去法(行に関するピボット選択(部分ピボッティング)あり)
* @param[inout] A n×nの係数項とn×1の定数項(b)を併せたn×(n+1)の行列.n+1列目に解が入る.
* @param[in] n n元連立一次方程式
* @return 1:成功
*/
int GaussEliminationWithPivoting(vector< vector<double> > &A, int n)
{
// 前進消去(forward elimination)
// - 対角要素をのぞいた左下要素をすべて0にする(上三角行列にする)
for(int k = 0; k < n-1; ++k){
// ピボット選択
Pivoting(A, n, k);
double akk = A[k][k];
for(int i = k+1; i < n; ++i){
double aik = A[i][k];
for(int j = k; j < n+1; ++j){
A[i][j] = A[i][j]-aik*(A[k][j]/akk);
}
}
}
// 後退代入(back substitution)
// - x_nの解はb_n/a_nn,x_nをさらにn-1行の式に代入することでx_(n-1)を求める.
// - この作業を1行目まで続けることですべての解を得る.
A[n-1][n] = A[n-1][n]/A[n-1][n-1];
for(int i = n-2; i >= 0; --i){
double ax = 0.0;
for(int j = i+1; j < n; ++j){
ax += A[i][j]*A[j][n];
}
A[i][n] = (A[i][n]-ax)/A[i][i];
}
return 1;
}
ガウス・ジョルダン法†ガウスの消去法の前進消去を拡張すると正方行列の逆行列を求めることができる. これは,ガウス・ジョルダン法(Gauss-Jordan method),もしくは,掃出し法(sweeping-out method)と呼ばれる. まず, さて,ガウスの消去法で対象とした連立1次方程式 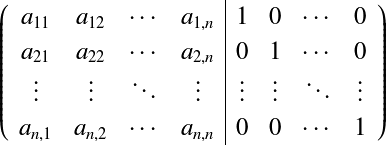
となる. つまり,拡大行列の左側半分が単位行列となるように変換することで,右側半分に逆行列ができる. 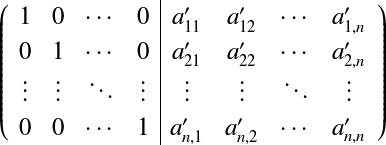 このとき,逆行列 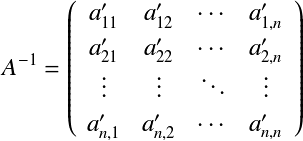 となる. 前進消去を拡張し,これらの処理を行うことで逆行列を求めるのが, ガウス・ジョルダン法である. ガウス・ジョルダン法の実装†ガウスの消去法における前進消去では上三角行列にするために,
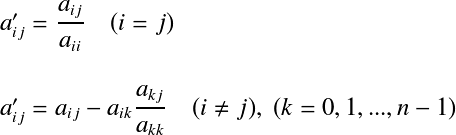 ガウス・ジョルダン法で逆行列を求めるコード例を以下に示す. /*!
* ガウス・ジョルダン法(ピボット選択なし)
* @param[inout] A n×2nの拡張行列
* @param[in] n n元連立一次方程式
* @return 1:成功
*/
int GaussJordan(vector< vector<double> > &A, int n)
{
// 拡張行列の右半分を単位行列にする
for(int i = 0; i < n; ++i){
for(int j = 0; j < n; ++j){
A[i][j+n] = (i == j ? 1.0 : 0.0);
}
}
// ガウス・ジョルダン法(Gauss-Jordan method)で逆行列計算
for(int k = 0; k < n; ++k){
double akk = A[k][k];
// 対角要素を1にするために,k行目のすべての要素をa_kkで割る
for(int j = 0; j < 2*n; ++j){
A[k][j] /= akk;
}
// k列目の非対角要素を0にする
for(int i = 0; i < n; ++i){
if(i == k) continue;
double aik = A[i][k];
for(int j = 0; j < 2*n; ++j){
A[i][j] -= A[k][j]*aik;
}
}
}
return 1;
}
参考文献†
|