![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
ヤコビ反復法†
以下に示す3元連立方程式を考える. 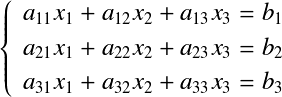 係数行列の対角成分 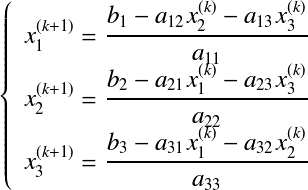 が導かれる.
ここで, このようにして解を求める方法がヤコビ反復法である.
解が収束したかどうかは また,相対誤差を用いた場合は, 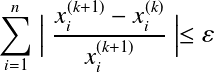 ここで また,反復法で問題となるのは収束するための条件である. そもそも収束しないのであれば反復を繰り返しても解が発散するだけである. 収束条件を上記の反復式から導出する. まず,反復式を以下のような形で表す. 反復回数が十分大きい数 この2つの式から以下が導かれる.
反復式から係数行列の要素を使って表すと, 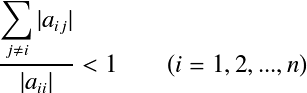 この式より,係数行列 ヤコビ反復法の実装†ヤコビ反復法をC++で実装した例を以下に示す. /*!
* ヤコビ反復法(Jacobi iterative method)
* - 解が収束するのは
* ・対角有利(diagonal dominant, 対角要素の絶対値>その行の他の要素の絶対値の和)
* ・係数行列が対称(symmetric)かつ正定(positive definite)
* のどちらかの場合
* @param[inout] A n×nの係数行列とn×1の定数項(b)を併せたn×(n+1)の拡大行列.n+1列目に解が入る.
* @param[in] n n元連立一次方程式
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int JacobiIteration(vector< vector<double> > &A, int n, int &max_iter, double &eps)
{
vector<double> x(n, 0.0); // 初期値はすべて0とする
vector<double> y(n, 0.0);
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 現在の値を代入して,次の解候補を計算
for(int i = 0; i < n; ++i){
y[i] = A[i][n];
for(int j = 0; j < n; ++j){
y[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
y[i] /= A[i][i];
}
// 収束判定
e = 0.0;
for(int i = 0; i < n; ++i){
e += fabs(y[i]-x[i]); // 絶対誤差の場合
//e += fabs((y[i]-x[i])/y[i]); // 相対誤差の場合
}
if(e <= eps){
break;
}
swap(x, y);
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = y[i];
}
return 1;
}
ガウス・ザイデル反復法†ヤコビ反復法では たとえば,3元連立1次方程式の場合,反復式は以下となる. 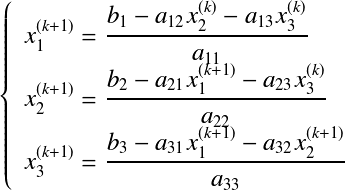 収束判定条件はヤコビ法と同じであり, 収束するための係数行列の条件も同じである. ただし,収束までの反復回数はヤコビ法よりも少なくすむ. ガウス・ザイデル反復法の実装†ヤコビ反復法では /*!
* ガウス-ザイデル反復法(Gauss Seidel iterative method)
* - 解が収束するのは
* ・対角有利(diagonal dominant, 対角要素の絶対値>その行の他の要素の絶対値の和)
* ・係数行列が対称(symmetric)かつ正定(positive definite)
* ・Σ_j |a_ij/a_ii| < 1 (i = 1〜n, j != i)
* @param[inout] A n×nの係数行列とn×1の定数項(b)を併せたn×(n+1)の行列.n+1列目に解が入る.
* @param[in] n n元連立一次方程式
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int GaussSeidel(vector< vector<double> > &A, int n, int &max_iter, double &eps)
{
vector<double> x(n, 0.0); // 初期値はすべて0とする
double tmp;
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 現在の値を代入して,次の解候補を計算
e = 0.0;
for(int i = 0; i < n; ++i){
tmp = x[i];
x[i] = A[i][n];
for(int j = 0; j < n; ++j){
x[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
x[i] /= A[i][i];
e += fabs(tmp-x[i]); // 絶対誤差の場合
//e += fabs((tmp-x[i])/tmp); // 相対誤差の場合
}
// 収束判定
if(e <= eps){
break;
}
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = x[i];
}
return 1;
}
SOR法†ヤコビ法やガウス・ザイデル法において各ステップで計算された 各ステップにおいて補正量 ここで, SOR法の実装†SOR法をC++で実装した例を以下に示す. /*!
* 逐次加速緩和法(SOR法:Successive Over-Relaxation)
* - ガウスザイデル反復法に加速係数をかけたもの
* @param[inout] A n×nの係数行列とn×1の定数項(b)を併せたn×(n+1)の行列.n+1列目に解が入る.
* @param[in] n n元連立一次方程式
* @param[in] w 加速緩和乗数 ([0,2])
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int SOR(vector< vector<double> > &A, int n, double w, int &max_iter, double &eps)
{
vector<double> x(n, 0.0); // 初期値はすべて0とする
double tmp;
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 現在の値を代入して,次の解候補を計算
e = 0.0;
for(int i = 0; i < n; ++i){
tmp = x[i];
x[i] = A[i][n];
for(int j = 0; j < n; ++j){
x[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
x[i] /= A[i][i];
x[i] = tmp+w*(x[i]-tmp);
e += fabs(tmp-x[i]); // 絶対誤差の場合
//e += fabs((tmp-x[i])/tmp); // 相対誤差の場合
}
// 収束判定
if(e <= eps){
break;
}
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = x[i];
}
return 1;
}
参考文献†
|