![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
|
非線形方程式の根を数値的に求める方法について 線形方程式と非線型方程式†
のような線形方程式(1次方程式)であるならば,その解は, と計算できる(ただし, 2次方程式( また,超越方程式(transcendental equation)と呼ばれる無限次代数方程式( 以下では非線形方程式を数値的に解く方法として,
について述べる. 2分法†関数 図1は2分法で近似解を求める手順を示している.
現在の解の存在区間を 2分法の手順を以下に示す.
反復を終了するための収束条件は以下となる. 2分法のコード例を以下に示す. /*!
* 2分法(bisection method)
* @param[in] func 関数値を与える関数ポインタ
* @param[in] xl,xr 探索範囲
* @param[out] x 解
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int bisection(double func(const double), double xl, double xr, double &x, int &max_iter, double &eps)
{
double f = func(xl);
double fmid = func(xr);
// 探索範囲の境界での値の符号が異なる場合のみ探索
if(f*fmid >= 0.0) return 0.0;
int k;
double dx = fabs(xr-xl), xmid;
for(k = 0; k < max_iter; ++k){
xmid = 0.5*(xl+xr); // 中点
dx *= 0.5;
// 中点での関数値を求める
fmid = func(xmid);
// 収束判定
if(dx < eps || fmid == 0.0){
x = xmid;
max_iter = k; eps = dx;
return 1;
}
// 新しい区間
if(f*fmid < 0){
xr = xmid;
}
else{
xl = xmid;
f = fmid;
}
}
max_iter = k; eps = dx;
return 0;
}
ニュートン・ラフソン法†2分法は指定した区間内の解は必ず求めるものの,解の収束は遅い.
関数 解の初期値を となる.この接線が
反復回数を多くすると限りなく となる. ニュートン法は2分法と異なり解のある区間でなく初期近似値1つだけを指定するだけでよく,収束も速い.
しかし, ニュートン法のコード例を以下に示す. /*!
* ニュートン・ラフソン法(Newton-Raphson method)
* @param[in] func 関数値を与える関数ポインタ
* @param[inout] x 探索開始位置を受け取り,解を返す
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int newton(double func(const double), double dfunc(const double),
double &x, int &max_iter, double &eps)
{
double f, df, dx;
int k;
for(k = 0; k < max_iter; ++k){
f = func(x);
df = dfunc(x);
x = xn-f/df;
// 収束判定
dx = fabs(f/df);
if(dx < eps || fabs(f) < eps){
max_iter = k; eps = dx;
return 1;
}
}
max_iter = k; eps = dx;
return 0;
}
多次元のニュートン・ラフソン法†ニュートン法を連立非線形方程式に一般化する. 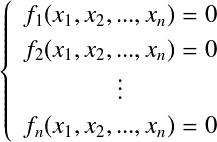 ベクトル表記では, ここで, である.
ここで,
が得られる.
この式は 例)2元連立非線形方程式の場合†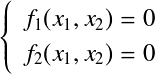 そして, 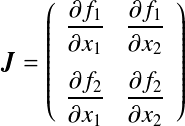 である.よって, 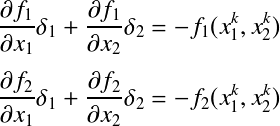
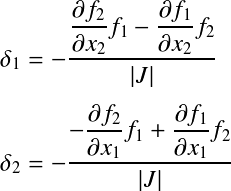 これらを用いて ホーナー法(組立除法)†2分法やニュートン法を使って以下の
乗算回数を少なくするために代数方程式を以下のように変形する. この場合,一番内側の括弧内から計算していくと, 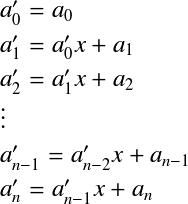 となり,最終的に ホーナー法で代数方程式の値とその導関数を求めるコード例を以下に示す. /*!
* ホーナー法で代数方程式の値を計算
* @param[in] x 変数
* @param[in] b 係数
* @param[in] n 方程式の次数
* @return 代数方程式の値
*/
template<class T>
inline T func_h(double x, const vector<T> &b, int n)
{
T f = b[0];
for(int i = 1; i <= n; ++i){
f = b[i]+f*x;
}
return f;
}
/*!
* ホーナー法で代数方程式の導関数値を計算
* @param[in] x 変数
* @param[in] b 係数
* @param[in] n 方程式の次数
* @return 代数方程式の導関数値
*/
template<class T>
inline T dfunc_h(double x, const vector<T> &b, int n)
{
T df = n*b[0];
for(int i = 1; i <= n-1; ++i){
df = (n-i)*b[i]+df*x;
}
return df;
}
テンプレート関数にしているのはDKA法で複素数を扱う関係上,様々な型に対応できるようにしたいためである. DKA法†代数方程式は重根も別々に考えると まず,代数方程式が複素解を持つとして,未知数を 代数方程式におけるニュートン法を考える.
上記の代数方程式の解を これを微分すると, 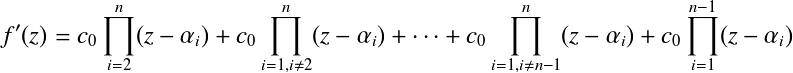
ここで, 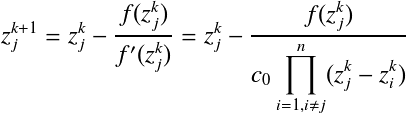 ここで, DK式により ここで, Aberthの初期値を用い,DK式を反復計算することで,
DKA法の手順†
Aberthの初期値の半径を求める方法は様々に提案されているが,ここでは
Aberthの方法*2を説明する.
ここで, の代数方程式を解いた時の解 DKA法を使って複数の根を一度に計算するコード例を以下に示す. まず,Aberthの初期値を求める関数である. /*!
* Aberthの方法で初期値を算出
* @param[out] z 解探索のための初期値
* @param[in] c 多項式の係数
* @param[in] n 方程式の次数
* @param[in] max_iter 半径計算のための最大反復数
* @param[in] eps 半径計算のための許容誤差
* @return 1:成功,0:失敗
*/
int aberth(vector<complexf> &z, const vector<complexf> &c, int n, int max_iter, double eps)
{
// 半径算出のための方程式の係数
vector<complexf> cd(n+1, 1.0); // 係数c'
double c1n = -c[1].real()/n;
cd[0] = c[0];
double rm; // 組立除法での余り
vector<double> a(n+1), tmp(n); // 係数格納用の一時的な変数
for(int i = 0; i <= n; ++i) a[i] = c[i].real();
// zの多項式をz+c1/nで割っていくことでwの多項式の係数を求める
for(int i = n; i > 1; --i){
horner(a, c1n, tmp, rm, i);
cd[i] = rm;
a = tmp;
}
cd[1] = a[1]+c1n;
// 多項式S(w)の係数
vector<double> b(cd.size());
b[0] = abs(cd[0]);
for(int i = 1; i <= n; ++i){
b[i] = -abs(cd[i]);
}
// Aberthの初期値の半径をニュートン法で算出
int m = 0; // 係数cの中で0でないものの個数
for(int i = 0; i <= n; ++i) m += (fabs(c[i].real()) > 1e-6 ? 1 : 0);
double rmax = 0.0; // 半径の最大値
for(int i = 1; i <= n; ++i){
double ri = pow(m*fabs(c[i].real())/fabs(c[0].real()), 1.0/(i+1.0));
if(ri > rmax) rmax = ri;
}
double r = rmax;
newton(b, n, r, max_iter, eps);
// Aberthの初期値
complexf zc = -c[1]/(c[0]*(double)n);
for(int j = 0; j < n; ++j){
double theta = (2*RX_PI/(double)n)*j+RX_PI/(2.0*n);
z[j] = zc+r*complexf(cos(theta), sin(theta));
}
return 1;
}
ここでは複素数を扱うために,C++のcomplexを使っている. #include <complex> // 複素数 typedef complex<double> complexf; 半径を算出するために,ニュートン法のコードを変更し,
係数列を与えると関数値と導関数値をホーナー法で計算するようにした.
また,半径算出のための /*!
* ホーナー法(組立除法)
- P(x) = a0 x^n + a1 x^(n-1) + ... + a_(n-1) x + a_n を (x-b) で割ったときの商と余りを返す
- 商はn-1次の多項式の係数として返す
* @param[in] a 代数方程式の係数
* @param[in] b 割る1次式の係数(x-b)
* @param[out] c 商であるn-1次の多項式の係数
* @param[out] rm あまり
* @param[in] n 方程式の次数(配列aの大きさはn+1,配列cはn)
*/
inline void horner(const vector<double> &a, double b, vector<double> &c, double &rm, int n)
{
if(n <= 1) return;
rm = a[0]; // 最終的に余りになる
c.resize(n);
for(int i = 1; i < n+1; ++i){
c[i-1] = rm;
rm *= b;
rm += a[i];
}
}
初期値を算出後,以下のワイヤストラス法の関数に多項式の係数とともに渡すことで解を得る. /*!
* ワイヤストラス法(DK公式)
* @param[inout] z 初期値位置を受け取り,解を返す
* @param[in] c 多項式の係数
* @param[in] n 方程式の次数
* @param[inout] max_iter 最大反復数(反復終了後,実際の反復数を返す)
* @param[inout] eps 許容誤差(反復終了後,実際の誤差を返す)
* @return 1:成功,0:失敗
*/
int weierstrass(vector<complexf> &z, const vector<complexf> &c, int n, int &max_iter, double &eps)
{
double e = 0.0, ej;
vector<complexf> zp;
complexf f, df;
int k;
for(k = 0; k < max_iter; ++k){
zp = z;
// DK式の計算
for(int j = 0; j < n; ++j){
f = func(z[j], c, n);
df = c[0];
for(int i = 0; i < n; ++i){
if(i != j){
df *= zp[j]-zp[i];
}
}
z[j] = zp[j]-f/df;
}
// 誤差の算出
e = 0.0;
for(int j = 0; j < n; ++j){
if((ej = abs(func(z[j], c, n))) > e){
e = ej;
}
}
// 収束判定
if(e < eps){
max_iter = k; eps = e;
return 1;
}
}
eps = e;
return 0;
}
Aberthの初期値について†代数方程式の解と係数の関係を導いてみる. まず,2次方程式の場合を考える. 解 元々の式と係数を比べることで,以下の関係式が得られる. 同様にしてn次方程式の場合, 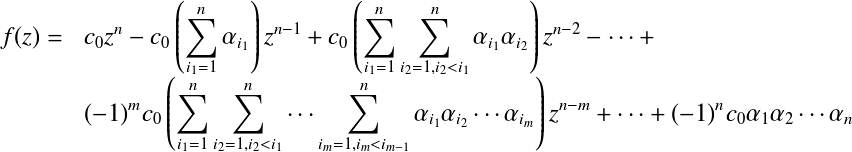 よって,n次方程式の解と係数の関係式は, ここで, 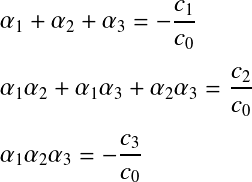
Aberthの初期値では解 を中心とした半径 となる.オイラーの公式( が得られる.ただし,ここでの ソースコード†上記のコードを含むVisual Studio 2010用のソースコードを以下に置く. 参考文献†
|